Short

Here is a rough sketch of why \(|\mathbb{R}^4| = |\mathbb{R}|\).

Actually, we'll explain something slightly simpler: that \(|\mathbb{R}^2| = |\mathbb{R}|\). From this simpler explanation, the argument for the more complicated case will be apparent, and likewise the argument for why \(|\mathbb{R}^n| = |\mathbb{R}|\) for any positive number \(n\).

Rather than construct a one-to-one correspondence between \(\mathbb{R}^2\) and \(\mathbb{R}\) directly, we're going to use a different technique.

Remember that \(\mathbb{R}\) is the continuous one-dimensional real line, and \(\mathbb{R}^2\) is the continuous two-dimensional plane. We can imagine a copy of \(\mathbb{R}\) sitting inside \(\mathbb{R}^2\), as the \(x\)-axis of a coordinate system. The elements of \(\mathbb{R}^2\) are of the form \([x, y]\), where \(x\) and \(y\) are real numbers. Then the \(x\)-axis is all the points of the form \([x, 0]\), where \(x\) is any real number. (The \(x\)-axis is exactly the points where the \(y\)-coordinate is zero.)

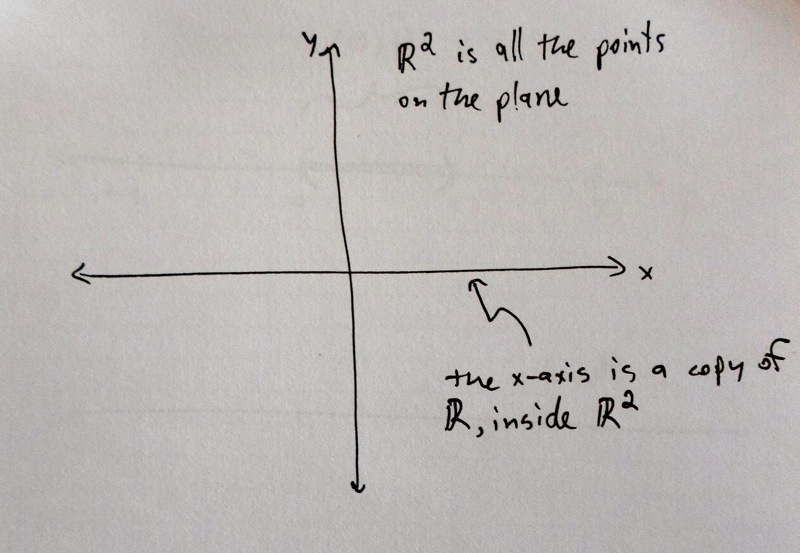
Figure: Coordinate axes drawn on a plane.

So we can construct a one-to-one correspondence between \(\mathbb{R}\) and the \(x\)-axis of the plane. Every real number \(x\) gets assigned to \([x, 0]\). This clearly hits every point on the \(x\)-axis once and only once. Since the \(x\)-axis is a subset of the whole plane \(\mathbb{R}^2\), we can conclude that \(|\mathbb{R}| ≤ |\mathbb{R}^2|\).

So far this isn't so surprising. But next we'll explain that \(|\mathbb{R}^2| ≤ |\mathbb{R}|\).

Every element of \(\mathbb{R}^2\) looks like \([x, y]\), for some real numbers \(x\) and \(y\). Make a rule that assigns each such pair to one real number, by interweaving the digits of \(x\) and \(y\). A few examples will give the idea.

\([0.111111…, 0.2222222…]\) gets assigned to \(0.1212121212…\).

\([13, 200]\) gets assigned to \(21030\).

\([485.2, 3.778]\) gets assigned to \(408053.270708\).

To do this carefully, we have to line up the digits of \(x\) and \(y\) so they have the same number of digits, and their decimal points match. This isn't a problem, since we can always add zeros to the left and right as needed. So we think of \([13, 200]\) as \([013.0, 200.0]\), and this gets assigned to \(021030\).

This rule assigns every element of \(\mathbb{R}^2\) to an element of \(\mathbb{R}\). It turns out that it doesn't actually hit every element of \(\mathbb{R}\) (read the In-Depth explanation to see why).

But the good news is that every element of \(\mathbb{R}\) it does hit, it only hits once. Another way of thinking of this is that we can undo the rule. From a real number like \(0.121212…\), it's possible to recover the point \([0.111…, 0.222…]\) that hit it. Just unweave the real number into two.

Because it is possible to unweave, we can conclude that our assignment rule makes a one-to-one correspondence between \(\mathbb{R}^2\) and a subset of \(\mathbb{R}\) (not all of \(\mathbb{R}\), because it doesn't hit everything). And this is enough to conclude that \(|\mathbb{R}^2| ≤ |\mathbb{R}|\).

It turns out that infinities work like regular numbers, in the sense that \(a ≤ b\) and \(b ≤ a\) means that \(a = b\). (This is actually a hard theorem to prove.)

So, since we have \(|\mathbb{R}| ≤ |\mathbb{R}^2|\) and \(|\mathbb{R}^2| ≤ |\mathbb{R}|\), we can conclude that \(|\mathbb{R}^2| = |\mathbb{R}|\).

You can read a short explanation of why \(|\mathbb{R}^4| = |\mathbb{R}|\), or an in-depth explanation (a rigorous proof), or you can take our word for it, and go read the story or the meta-discussion.

Short Version Meta Discussion In-Depth Version True Story

Short

NEXT