Sets and Size
The best way to think about size is in terms of sets.
The best way to think about size is in terms of sets. A set is a collection of objects. Every set has a size (also called its cardinality). We can write a set by listing its elements inside of brackets \(\{\cdots\}\).
For example, one set is \(\{a, b, c\}\). Another set is \(\{2, 3, 4, 5\}\). Another is \(\{\triangle, \bigcirc\}\). Given a set, we can talk about its subsets; for example, the sets \(\{b\}\) and \(\{a, b\}\) are two subsets of \(\{a, b, c\}\).
The cardinality of the set \(\{a, b, c\}\) is, believe it or not, three. We would write this by adding bars around the set, so the equation:
\[\left|\{a, b, c\}\right| = 3\]
is exactly the statement "The size of the set \(\{a, b, c\}\) is three."
When the size of a set is a finite number, like three, we say it is a finite set. An infinite set is a set that is not finite.
The Natural Numbers \(\mathbb{N}\)
The numbers \(\{0,1,2,3,...\}\) form the simplest infinite set.
Now consider the set \(\{0, 1, 2, 3, 4,...\}\).
The "…" means to keep going in this manner, i.e. collect zero and all the positive numbers like this, and put them into one set. This is an important set, called the set of natural numbers, and denoted by the symbol \(\mathbb{N}\). (We want to talk about all of them at once, so we assume that this metaphorical collecting process has been done and is over; every positive natural number is in the set.)
So what is \(|\mathbb{N}|\)? That is, what is the size of the natural numbers? Well, it's not a finite number; it's bigger than every finite number. So, by definition, the size of \(|\mathbb{N}|\) is infinite.
There are other infinite sets. For example, the set of all even natural numbers, i.e.: \(\{0, 2, 4, 6, 8, 10,...\}\). This set is usually written \(2\mathbb{N}\). At this point, all we can say is that \(|2\mathbb{N}|\) is infinite, since it's going to be bigger than any finite number. The "…" means "keep going forever like this".
But is \(|\mathbb{N}|\) bigger than \(|2\mathbb{N}|\)? Or are they the same size? Notice that \(2\mathbb{N}\) is a subset of \(\mathbb{N}\). That is, everything in \(2\mathbb{N}\) (for example the number \(4\)) is also in \(\mathbb{N}\). Our intuition might suggest that \(\mathbb{N}\) has to be "bigger".
Then again, maybe infinity doesn't care if you grow towards it slowly or fast. Maybe the "…" in \(2\mathbb{N}\) means that, in some sense, \(2\mathbb{N}\) can catch up to \(\mathbb{N}\), and we should say that both are the same size. Isn't infinity infinite, end of story?
One-to-one Correspondences
Two sets are the same size if there is a one-to-one correspondence between them.
The mathematician who succeeded in making sense of infinity is Georg Cantor, a German working in the second half of the nineteenth century. He recognized the key question was: What should it mean for two sets to be the same size? And he answered this question: Two sets are the same size if there is a one-to-one correspondence between them. To mathematicians, this has become the definition of "having the same size".
A one-to-one correspondence is basically just what it sounds like: a rule for assigning elements of two sets to each other, in such a way that every element in one set corresponds with exactly one element in the other.
For example, there is a 1-1 correspondence between the sets \(\{a, b, c\}\) and \(\{4, 5, 6\}\), assigning \(a\) to \(4\), \(b\) to \(5\), and \(c\) to \(6\). There's a different 1-1 correspondence, assigning \(a\) to \(6\), \(b\) to \(5\), and \(c\) to \(4\). These 1-1 correspondences can have some degree of arbitrariness to them. We don't ask how many different ones are there. We ask whether or not at least one exists.
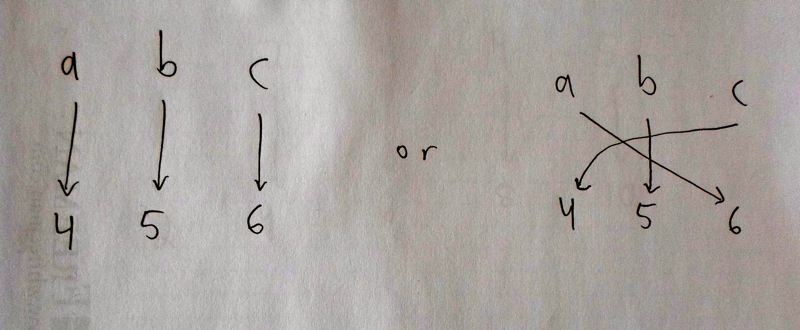
In the example just given, we found a 1-1 correspondence. Therefore, we say the two sets have the same size. And in this case, our intuition agrees. The size is three. Every set of three elements will have a 1-1 correspondence with every other set of three elements. They all have size three.
On the other hand, consider trying to make a 1-1 correspondence between the sets \(\{a, b, c, d\}\) and \(\{4, 5, 6\}\). It can't be done. Two things in the first set would have to be assigned to the same element in the second; this isn't one-to-one. Or going in the other direction, by assigning \(4\) and \(5\) and \(6\), you won't be able to hit everything in \(\{a, b, c, d\}\). No matter how hard you try, you won't be able to make a 1-1 correspondence. Thus the two sets aren't the same size. Another way to say it: four isn't equal to three.
So we see that Cantor's definition agrees with our intuition, when it comes to finite sets.
But now let's think about infinite sets. Are \(\mathbb{N}\) and \(2\mathbb{N}\) the same size?
According to Cantor, we should try to make a 1-1 correspondence between the elements of \(\mathbb{N}\) and the elements of \(2\mathbb{N}\). And, after some reflection, this is possible. The easiest way is assigning zero to zero, \(1\) to \(2\), \(2\) to \(4\), \(3\) to \(6\), \(4\) to \(8\), etc.
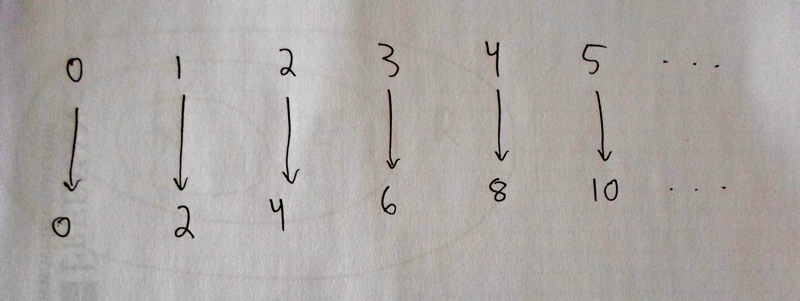
We need to be careful, and really convince ourselves that by repeating this pattern (every number in \(\mathbb{N}\) goes to its double in \(2\mathbb{N}\)), we will hit everything in \(2\mathbb{N}\), and hit it exactly once. It works. Do you agree? This 1-1 correspondence does the job, and so the two sets are the same size. That is, \(|\mathbb{N}| = |2\mathbb{N}|\).
The notion of one-to-one correspondence is crucial to everything on this site. To review: we will look at different types of infinite sets, and ask if they are the same size or not. To show two sets are the same size, we need to show that there exists some one-to-one correspondence between them. On the other hand, if we want to show two sets are not the same size, we need to show that no matter how hard we, or anyone else, tries, no one-to-one correspondence can be made.
Integers \(\mathbb{Z}\), Real Numbers \(\mathbb{R}\)
Two more important examples of infinite sets.
We will end this overview by giving a few more important examples of infinite sets that we’ll need to use, and one more example of a one-to-one correspondence.
The set of integers is defined to be the set:
\[\{..., -3, -2, -1, 0, 1, 2, 3, ...\}.\]
This is denoted by \(\mathbb{Z}\).
The set of real numbers, denoted by \(\mathbb{R}\), is all the points on a continuous line. Another way to think of them is as all the decimals. That is, numbers like \(1.25\), \(-3.2\), \(2.0\), \(0.4444444...\), etc. To the left of the decimal point is an integer (in these examples, \(1\), \(-3\), \(2\), and \(0\)). To the right of the decimal point can be a never-ending string of digits (as with \(0.44444...\); the "\(...\)" means that it's \(4\)s all the way out). The famous number \(\pi\) is also an example of a real number.
Notice that every natural number is an integer, and every integer is a real number.

When thinking about all these sets, it's useful to visualize a line, extending to the left and right indefinitely. Zero is a point somewhere in the middle. The natural numbers are evenly spaced discrete points, going to the right. The integers include the natural numbers, but also go off to the left. The real numbers are all the points on the line.

What are the sizes of \(|\mathbb{Z}|\) and \(|\mathbb{R}|\)? Right now, let's just consider \(|\mathbb{Z}|\). Is \(\mathbb{Z}\) the same size as \(\mathbb{N}\)? In other words, can we make a one-to-one correspondence between the two sets?
The answer is yes. Here's the start of one such correspondence:
\[0 \leftrightarrow 0 \\ 1 \leftrightarrow 1\\ 2 \leftrightarrow -1\\ 3 \leftrightarrow 2\\ 4 \leftrightarrow -2\\ 5 \leftrightarrow 3\\ 6 \leftrightarrow -3\\ 7 \leftrightarrow 4\\ 8 \leftrightarrow -4\]
Notice that making a one-to-one correspondence of \(\mathbb{Z}\) with the set \(\mathbb{N}\) is like making a list of the elements of \(\mathbb{Z}\) in a systematic way, so that everything in \(\mathbb{Z}\) appears exactly once.
Take some time to be sure you understand what the assignment "rule" or "pattern" is. Then convince yourself that this does the job, that everything in N gets assigned to exactly one thing in \(\mathbb{Z}\), and that nothing in \(\mathbb{Z}\) gets left out. We've just proved that \(|\mathbb{N}| = |\mathbb{Z}|\).
Product Sets
Product sets multiply two sets together. These appear in the first and fourth modules.
Now you're ready to take on stranger infinite sets. There’s one more type that we’ll explain here; you only need this for the first and fourth modules.
Given two sets, we can make their product set by taking pairs of elements. We write it with a \(\times\) sign.
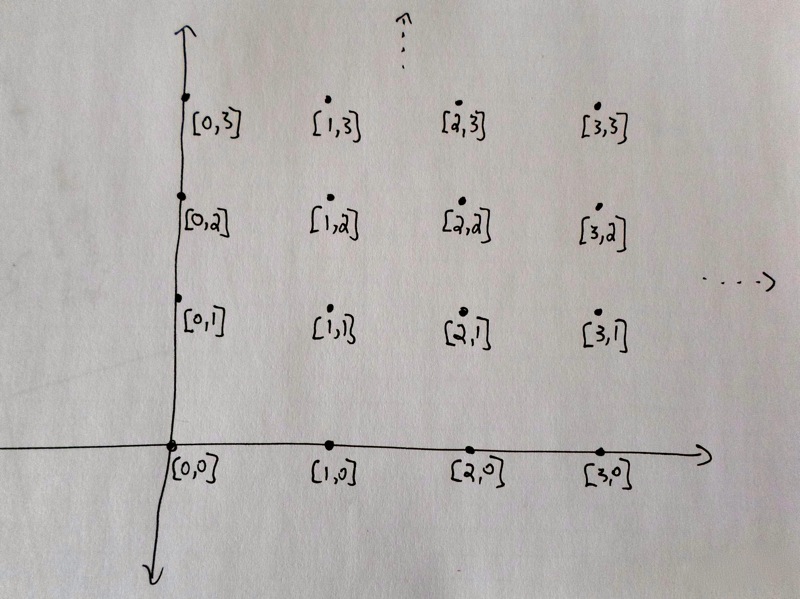
So \(\mathbb{N}\times\mathbb{N}\) means the set of pairs \([a, b]\), where \(a\) is an element of \(\mathbb{N}\) and \(b\) is also an element of \(\mathbb{N}\).
And \(\mathbb{R}\times\mathbb{R}\) means the set of pairs \([a, b]\) where \(a\) and \(b\) are elements of \(\mathbb{R}\).
(It is more standard to use the notation \(\left(a,b\right)\), but this notation also gets used for other things so we’re sticking with \([a,b]\) to indicate a pair of elements.)
You can visualize \(\mathbb{R}\times\mathbb{R}\) as all the points on a plane -- like a never-ending piece of paper. Each point has coordinates \([x, y]\). Then \(\mathbb{N}\times\mathbb{N}\) is a subset of this plane, and looks like a grid of discrete points with one corner at \([0, 0]\), going off forever to the right and up and right-and-up. From the picture, you can think of \(\mathbb{N}\times\mathbb{N}\) as \(\mathbb{N}\) copies of \(\mathbb{N}\). The picture looks like this.