Short

Our goal here is to get a rough idea as to why \(|\mathbb{N}\times\mathbb{N}| = |\mathbb{N}|\).

In a sense, you could think of this as saying that "infinity times infinity is still just infinity." But this is not very precise, and a key point of this site is that we need to be careful distinguishing different types of infinity.

Recall that \(\mathbb{N}\times\mathbb{N}\) is the set of pairs of the form \([a, b]\), where \(a\) and \(b\) are elements of \(\mathbb{N}\). We can think of it as \(\mathbb{N}\) copies of \(\mathbb{N}\).

Remember that to show that \(|\mathbb{N}\times\mathbb{N}| = |\mathbb{N}|\), we need to construct a one-to-one correspondence between the set \(\mathbb{N}\times\mathbb{N}\) and the set \(\mathbb{N}\). In the section on set theory basics, we saw that making a one-to-one correspondence with \(\mathbb{N}\) is like making a list of elements, so that everything appears exactly once. If we wanted to list all the elements of \(\mathbb{N}\times\mathbb{N}\), how would we do it?

The key insight is to display the elements of \(\mathbb{N}\times\mathbb{N}\) in a clever way, and use this to make the list. Remember in the overview we mentioned we can think of this set as a grid on a plane.

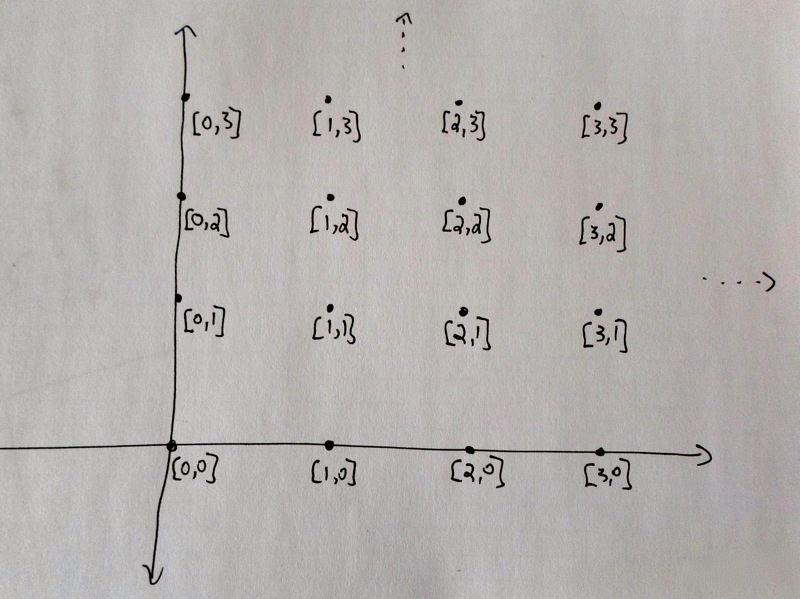
Figure: Plane with uniform lattice of points.

Now we can start assigning elements of \(\mathbb{N}\times\mathbb{N}\) in the corner, at \([0, 0]\), and working right and up along diagonals. How exactly we do this is somewhat arbitrary, we just have to be sure not to skip anything in \(\mathbb{N}\times\mathbb{N}\).

Figure: Plane with uniform lattice of points, and zigzagging arrows.

Then according to this assignment rule, the beginning of our list would look something like the following.

\[0 \leftrightarrow [0,0]\\ 1 \leftrightarrow [1, 0]\\ 2 \leftrightarrow [0, 1]\\ 3 \leftrightarrow [0, 2]\\ 4 \leftrightarrow [1, 1]\\ 5 \leftrightarrow [2, 0]\\ 6 \leftrightarrow [3, 0]\\ 7 \leftrightarrow [2, 1]\]

By looking at the picture, and the list, we can convince ourselves that every element in \(\mathbb{N}\) is getting assigned to exactly one element of \(\mathbb{N}\times\mathbb{N}\), and everything in \(\mathbb{N}\times\mathbb{N}\) is hit at some point. Therefore we have a one-to-one correspondence! Thus \(|\mathbb{N}\times\mathbb{N}| = |\mathbb{N}|\).

You can read a short explanation of why \(|\mathbb{N}\times\mathbb{N}|=|\mathbb{N}|\), or an in-depth explanation (a rigorous proof), or you can take our word for it, and go read the story or the meta-discussion.

Short Version Meta Discussion In-Depth Version True Story

Short

NEXT